The Kohn–Sham formalism provides a practical framework for implementing Density Functional Theory (DFT) by introducing a fictitious system of non-interacting electrons that yields the same ground-state electron density as the true interacting system.
Motivation
While the Hohenberg–Kohn theorems establish the existence of a universal energy functional $F[\rho]$, they do not provide an explicit form for it. The Kohn–Sham approach circumvents this issue by splitting the functional into known and unknown parts, allowing the ground-state properties to be determined via self-consistent single-particle equations.
Decomposition of the Energy Functional
The total energy functional is written as: \begin{equation} E[\rho] = T_s[\rho] + E_{\mathrm{H}}[\rho] + E_{\mathrm{xc}}[\rho] + \int V_{\mathrm{ext}}(\mathbf{r}) \rho(\mathbf{r}) , d\mathbf{r}, \end{equation} where:
$T_s[\rho]$ is the kinetic energy of a system of non-interacting electrons with density $\rho(\mathbf{r})$.
$E_{\mathrm{H}}[\rho]$ is the classical electrostatic (Hartree) energy: \begin{equation} E_{\mathrm{H}}[\rho] = \frac{1}{2} \int \int \frac{\rho(\mathbf{r}) \rho(\mathbf{r’})}{|\mathbf{r} - \mathbf{r’}|} , d\mathbf{r} , d\mathbf{r’}. \end{equation}
$E_{\mathrm{xc}}[\rho]$ is the exchange-correlation energy functional, which includes all many-body effects: exchange, correlation, and the difference between the true kinetic energy and $T_s[\rho]$.
The Kohn–Sham Ansatz
Assume that the ground-state density $\rho(\mathbf{r})$ can be represented by a set of single-particle orbitals ${ \phi_i(\mathbf{r}) }$ such that: \begin{equation} \rho(\mathbf{r}) = \sum_{i=1}^{N} |\phi_i(\mathbf{r})|^2, \end{equation} where the orbitals $\phi_i$ are solutions of a fictitious system of non-interacting particles.
Derivation of the Kohn–Sham Equations
To find the orbitals that minimize the energy functional under the constraint of orthonormality, \begin{equation} \langle \phi_i | \phi_j \rangle = \delta_{ij}, \end{equation} we perform a constrained minimization using Lagrange multipliers. The functional to minimize is: \begin{equation} \mathcal{L} = E[\rho] - \sum_{i,j} \lambda_{ij} \left( \langle \phi_i | \phi_j \rangle - \delta_{ij} \right). \end{equation}
Taking functional derivatives with respect to $\phi_i^*(\mathbf{r})$ leads to the Euler–Lagrange equations: \begin{equation} \left[ -\frac{1}{2} \nabla^2 + V_{\mathrm{eff}}(\mathbf{r}) \right] \phi_i(\mathbf{r}) = \epsilon_i \phi_i(\mathbf{r}), \end{equation} where the effective potential $V_{\mathrm{eff}}(\mathbf{r})$ is defined as: \begin{equation} V_{\mathrm{eff}}(\mathbf{r}) = V_{\mathrm{ext}}(\mathbf{r}) + V_{\mathrm{H}}(\mathbf{r}) + V_{\mathrm{xc}}(\mathbf{r}). \end{equation}
Here,
- $V_{\mathrm{H}}(\mathbf{r}) = \int \frac{\rho(\mathbf{r’})}{|\mathbf{r} - \mathbf{r’}|} , d\mathbf{r’}$ is the Hartree potential,
- $V_{\mathrm{xc}}(\mathbf{r}) = \frac{\delta E_{\mathrm{xc}}[\rho]}{\delta \rho(\mathbf{r})}$ is the exchange-correlation potential.
Self-Consistent Solution Procedure
Now, we can see that $V_{eff}(r)$ depends on $\rho(r)$. But, $\rho(r)$ depends on the Kohn-Sham orbital, $\psi(r)$, which depend on $V_{eff}(r)$, which creates a circular dependency. We solve this using self consistent field (SCF) method.
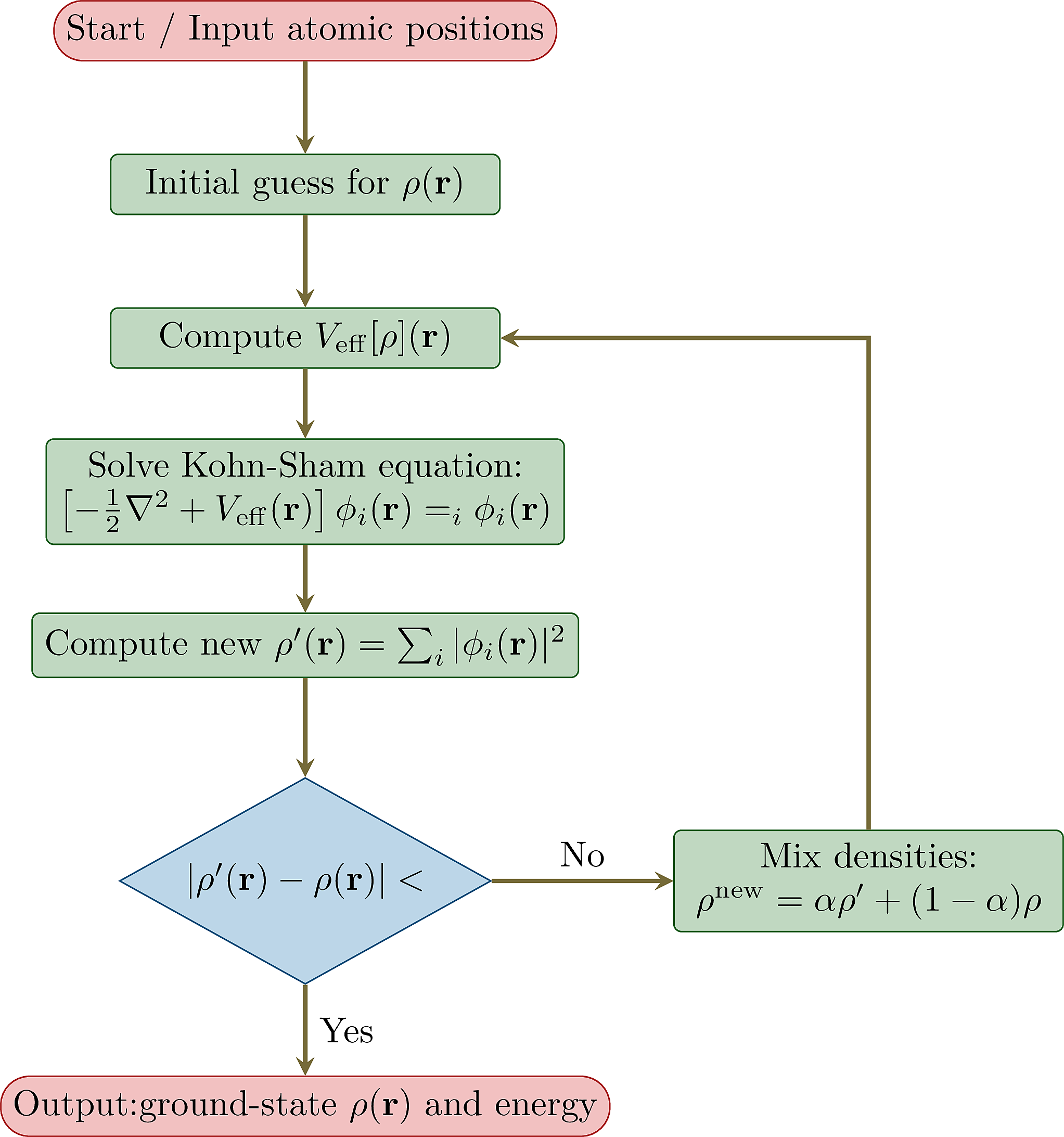
The Kohn–Sham equations are solved self-consistently using the following iterative loop:
- Start with an initial guess for the electron density $\rho^{(0)}(\mathbf{r})$.
- Construct the effective potential $V_{\mathrm{eff}}^{(n)}(\mathbf{r})$.
- Solve the Kohn–Sham equations to obtain the orbitals $\phi_i^{(n)}(\mathbf{r})$.
- Compute the new density: \begin{equation} \rho^{(n+1)}(\mathbf{r}) = \sum_{i=1}^N |\phi_i^{(n)}(\mathbf{r})|^2. \end{equation}
- Check for convergence. If not converged, return to step 2.
Remarks
- The Kohn–Sham approach allows the use of efficient single-particle methods to capture the ground-state properties of an interacting system.
- All complexities of exchange and correlation are absorbed into $E_{\mathrm{xc}}[\rho]$, which must be approximated (e.g., using LDA, GGA, etc.).
- The eigenvalues $\epsilon_i$ do not have rigorous physical interpretation except for the highest occupied orbital, which (under some assumptions) equals the negative of the ionization energy.